一、检验的一般步骤
1.资料 这里所要的是类似第七章第一节三、中所述的成组资料,不过现在不是两组而是多组,如下例。
例8.1 分泌型免疫球蛋白A(SIgA)是胃肠道分泌液、泪液等外分泌液中的主要免疫球蛋白类,某院研制了“125I-SIgA放射免疫测定药盒”,为人体SIgA的检验提供了一种简便方法。为比较不同批号药盒检验结果是否一致,该院曾将三批号各四个药盒一一测定了某一标本得结果如下,试作方差分析。
表8.1 三个批号药盒的SIgA放射免疫测定值
| 批号 | SIgA含量(μg/ml), X | ∑X | n | X | ∑X2 | ∑X2-(∑X)2/n | |||
| 1 | 1.92 | 1.80 | 2.08 | 2.00 | 7.80 | 4 | 1.95 | 15.2528 | 0.0428 |
| 2 | 2.21 | 2.25 | 2.12 | 2.57 | 9.15 | 4 | 2.29 | 21.0459 | 0.1153 |
| 3 | 3.27 | 2.75 | 2.90 | 3.10 | 12.02 | 4 | 3.01 | 36.2754 | 0.1553 |
| 合计 | 28.97 | 12 | 2.414 | 72.5741 | 0.3134 | ||||
2. 分析 从表8.1的测定结果可以看出这里有三种变异:
(1)从同一批号药盒的四次测定结果看,不尽相同,这是组内变异。显然它不是由于批号不同的影响,而只是由于误差(如批内各药盒的差异性和测量误差等)造成的。
(2)从各批测定值的均数来看,是不相同的,这是组间变异,表明各批药盒性能质量也许对测得的结果有一定影响,也包括误差的作用。
(3)12次测定的SIgA含量都不尽相同,有高有低,它们既可能受药盒来自不同批号的影响,也包括组内变异,因此称为总变异。
那么这里各批药盒测SIgA均值间的差别,只不过是抽样误差的反映呢?还是药盒制作质量不稳定,批间存在显著差别?为了得出正确的结论,可进行方差分析。方差分析的基本甲思想是:①从总变异中分出组间变异和组内变异,并用数量表示变异的程度;②将组间变异和组内变异进行比较,如两者相差不大,说明受批号不同的影响不大;如果两者相差较大,组间变异比组内变异大得多,说明批号不同的影响不容忽视。下面我们根据表8.1资料来计算这三种变异。
(1)总离均差平方和:即12个观察值各与总均数相差的平方之和,公式为
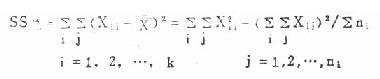
(8.1)
式中SS总即总离均差平方和,Xij表示第i组的第j个观察值,X为全部观察值的平均数,k是组数。
本例SS总=72.5741-28.972/12=2.6357
(2)组间离均差平方和:即取各组均数代替该组各观察值后,它们分别与总均数相差的平方之和,公式为
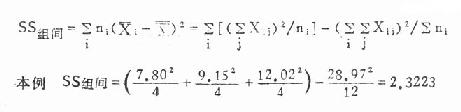
(8.2)
(3)组内离均差平方和:只要加总各组本身的离均差平方和即得,公式为
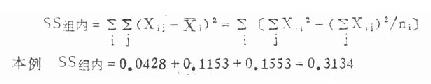
(8.3)
由本例计算结果可以看出,SS组间+SS组内=SS总,如2.3223+0.3134=2.6357。因此,算出SS总以后再计算SS组间、SS组内两者中之一个,其余一个便可通过减法求得。
将以上求得的几种变异各除以自由度后得均方。自由度的计算公式分别为
总变异 N-1 (N为各组例数之和)( 8.4)
组间变异 K-1 (8.5)
组内变异 N-K (8.6)
组间均方与组内均方之比为F值,
F=组间均方/组内均方 (8.7)
本例
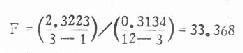
将以上数据列入下面的方差分析表可使人一目了然。
表8.2 方差分析表
| 变异来源 | 离均差平方和 | 自由度 | 均 方 | F |
| 总 变 异 | 2.6357 | 11 | ||
| 组间变异 | 2.3223 | 2 | 1.1612 | 33.368 |
| 组内变异 | 0.3134 | 9 | 0.0348 |
如果求得的F值小于1或略大于1,也即组间变异与组内变异差不多,则关于不同批药盒所致影响就不值得注意,反之,若各批均数间差别甚大,组间变异比组内变异大得多,说明不能只把它看成为误差的表面,很可能不同批药盒的测定值具有差别。现F值远大于1,若等于或大于某α水准下的临界F值,便将拒绝检验假设H0而接受备择假设H1。
本例定α=0.05,查附表8F值表,F0.05(2,9)=4.26。括弧内2为求F值时分子(也即较大均方)的自由度,9为分母的自由度,今F=33.368,远大于此临界值4.26,故P<0.05,说明不同批药盒的影响不容忽视,各批药盒测定的SIgA值相差显著。
二、多个均数间的两两比较
经方差分析(即F检验),若各组均数之间差别不显着,则到此为止,不必作进一步统计学处理了。当F检验结果为相差显着时,这只是对各组均数的整体而言,至于哪些均数间的差别显着,哪些不显着,还要作如下进一步分析。
本例检验结果为相差显着,这里我们先用较为简单而实用的最小显着差数法来比较三组中每两组均数间的差别是否显着,然后介绍q值法。
1.最小显着差数法
(1)计算最小显着性差数Dα,ν
Dα,ν=t,
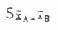
(8.8)
式中t,由附表3查得,查时自由度ν用方差分析表中组内变异的自由度,本例为9;α即显著性水准,常用0.05或0.01,本例查得两个临界t值即t0.05,9=2.262,t0.01,9=3.250。标准误
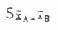
的计算公式是
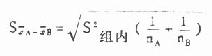
(8.9)
S2组内也即表8.2中的组内均方(也可叫误差均方)0.0348。nA、nB为所比较的两组的例数,本例各组例数都为4。现将数据代入式(8.9)、(8.8)求得
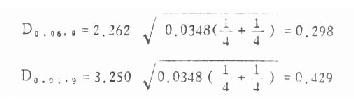
(2)用上述的最小显著性差数与每两组均数的相差数比,若后者大于前者(临界值),便相差显著,若小于前者,为相差不显著。现将两均数间的比较结果列于下表。
表8.3 均数间两两比较
| A与B(批号) | ∣XA-XB∣ | 界 值 | P值 | |
| D0.05 | D0.01 | |||
| 1与2 | 0.34 | 0.298 | 0.429 | <0.05 |
| 1与3 | 1.06 | 0.298 | 0.429 | <0.01 |
| 2与3 | 0.72 | 0.298 | 0.429 | <0.01 |
注:表中XA-XB两侧的直杠是绝对值符号。
3.统计结论:各批间均在α=0.05水准处相差显著,又第3批与第1、2两批比,P<0.01,说明各批药盒对SIgA的检测效果不一致,批号3远高于批号2与1。
上面介绍的多个均数间两两比较的方法虽较简便,精确性有时不足,尤其当比较的均数不是在三个而是更多,或各样本含量不相等时应用也较麻烦。下面介绍查临界q值而不查t值的另一比较方法。
2.q值法
(1)将表8.1中三个均数自大至小排列得:
| 第3批 | 第2批 | 第1批 | |
| SIgA平均值,X(μg/ml) | 3.01 | 2.29 | 1.95 |
| 秩次 | 1 | 2 | 3 |
| 样本含量,n | 4 | 4 | 4 |
(2)用组内均方与平均每组例数n0求出标准误,然后与由附表9中查到的临界q值相乘,即可列出比较表加以比较。下面是求平均例数的公式。
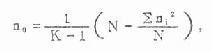
(i=1,2,…,k) (8.10)
此例
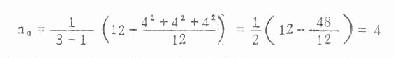
本例各组样本大小相等,均为4,本无须用上式计算,但若各组大小不等时就得用上式求平均例数。
标准误公式为
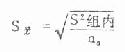
(8.11)
此例
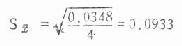
表8.4 均数间两两比较
| A与B
(秩次) | 组数α | ∣XA-XB∣ | Q0.05(a,ν)Sχ | ν见组内变异一行
P值 |
| 3与2 | 2 | 0.34 | 0.299 | <0.05 |
| 3与1 | 3 | 1.06 | 0.369 | <0.05 |
| 2与1 | 2 | 0.72 | 0.299 | <0.05 |
现将上表栏目自左至右一一说明如下:
表内左侧,均数大小秩次3与2比,即相邻两组相比,故组数a等于2。同样,第三行的2与1比,因2与1相邻,a也是2,3与1比则由3到1组数有3,a等于3。关于查附表9中的q值,一方面根据该表上端横行a的数字,另方面根据表左侧直行的ν,也即方差分析表中组内(或误差)项的自由度(本例为9)来查。表内q值有上、下两行数,若定α为0.05,查上行,α为0.01则查下行。
就本例言,用两种方法作均数间两两比较,其结论完全一致。
例8.2 下表为用动物研究白血病时测得的鼠脾DNA(脱氧核糖核酸)含量,现作方差分析,比较四个不同病情组的均数相差是否显著。
表8.5 鼠脾DNA含量测定值(mg)
| 正常组 | 患自发性
白血病组 | 患移植白血病 | 总 计 | ||
| 甲组 | 乙组 | ||||
| 12.3 | 10.8 | 9.3 | 9.5 | ||
| 13.2 | 11.6 | 10.3 | 10.3 | ||
| 13.7 | 12.3 | 11.1 | 10.5 | ||
| 15.2 | 12.7 | 11.7 | 10.5 | ||
| 15.4 | 13.5 | 11.7 | 10.5 | ||
| 15.8 | 13.5 | 12.0 | 10.9 | ||
| 16.9 | 14.8 | 12.3 | 11.0 | ||
| 17.3 | 12.4 | 11.5 | |||
| 13.6 | |||||
| ∑Xij j | 119.8 | 89.2 | 104.4 | 84.7 | 398.1 |
| ni | 8 | 7 | 9 | 8 | 32 |
| Xi | 14.98 | 12.74 | 11.60 | 10.59 | 12.44 |
| ∑X2ij j | 1815.96 | 1147.32 | 1223.58 | 899.15 | 5086.01 |
| SSi | 21.96 | 10.66 | 12.54 | 2.39 | 47.55 |
1.作检验假设H0:μ1=μ2=μ3=μ4,H1:各总体均数不都相等。α=0.01。
2.用表8.5下部数字计算离均差平方和:简法是先求校正数C=(∑X)2/N=398.12/32,再求
SS总:5086.01-(398.1)2/32=133.40
SS组间:(119.8)2/8+(89.2)2/7+(104.4)2/9+(84.7)2/8-(398.1)2/32=85.85
SS组内:133.40-85.85=47.55
3.列出方差分析表
表8.6 方差分析表
| 变异来源 | 自由度 | 离均差平方和 | 均方 | F |
| 总 计 | 31 | 133.40 | ||
| 组 间 | 3 | 85.85 | 28.62 | 16.48 |
| 组 内 | 28 | 47.55 | 1.70 |
4.查F值表,下结论。看附表8(3),根据求F值时组间均方较大,于是用其自由度3及组内均方的自由度28查得F0.01(3,28)=4.57,今F=16.84>F0.01(3,28)=4.57,故在α=0.01水准处相差显著,P<0.01。四组鼠脾的DNA含量不等。(注:F小于1时无须查表)。
5.为详细分析每两组间的相差情况,作两两比较如下。(因各组例数不等又组数较多,故用Q值法比较)。
(1)将四组均数按大小排列:
| 正常组 | 患白发性
白血病组 | 患移植白血病 | ||
| 甲组 | 乙组 | |||
| DNA平均含量(mg) | 14.98 | 12.74 | 11.60 | 10.59 |
| 秩次 | 1 | 2 | 3 | 4 |
| 样本含量,n | 8 | 7 | 9 | 8 |
(2)求平均例数与标准误:由式(8.10)与式(8.11)计算得
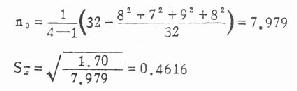
(3)列表比较:
表8.7 均数间两两比较
| A与b
(秩次) | 组数a | ∣XA-XB∣ | 界 值 | P值 | |
| q0.05Sχ | q0.01Sχ | ||||
| 4与3 | 2 | 1.01 | 1.36 | 1.86 | >0.05 |
| 4与2 | 3 | 2.15 | 1.65 | 2.14 | <0.01 |
| 4与1 | 4 | 4.39 | 1.83 | 2.32 | <0.01 |
| 3与2 | 2 | 1.14 | 1.36 | 1.86 | >0.05 |
| 3与1 | 3 | 3.38 | 1.65 | 2.14 | <0.01 |
| 2与1 | 2 | 2.24 | 1.36 | 1.86 | <0.01 |
注:本例组内均方的自由度为28但q值表中左侧无28,故用邻近的较小自由度20,此外也可用内插法求出γ为28的q值。
比较结果,除患移植性白血病甲、乙组间;甲组与自发性白血病组间(即按均数大小秩次3与4、3与2间)相差不显著外,余均在α=0.01水准处相差显著,说明正常鼠脾DNA含量最高,患移植白血病乙组的最低。
