一、一元弱酸弱碱的离解平衡
(一)离解度和离解常数
一元弱酸弱碱(如HOAc,NH3等)是弱电解质,在溶液中只能部分离解。离解程度用离解度表示。
离解度是指溶液中已经离解的电解质的分子数占电解质总分子数(已离解的和未离解的)的百分数。通常用α表示。

一元弱酸HA存在以下的离解平衡:
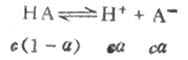
平衡浓度为
c(1-α) cα cα其中c为HA的总浓度,α为离解度。
离解常数KI可表示为

(2-1)
KI在一定温度下为一常数,不能随浓度变化而变化。弱酸的离解常数习惯上用Ka表示,弱碱的离解常数用Kb表示。
如果弱电解质离解度α很少,则
1-α≈1
这时式(2-1)为
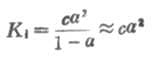
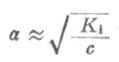
(2-2)
从式(2-2)可以看出,在一定温度下,同一弱电解质的离解度大约与溶液浓度的平方根成反比,即离解度随溶液的稀释而升高。这条说明溶液浓度与离解度关系的定律,叫做稀释定律。式(2-2)叫做稀释定律公式。利用此公式可以进行有关离解试或离解常数的计算。
例1在25℃时,已知(1)0.1mol·L-1HOAc的离解度为1.32%;(2)0.2mol·L-1HOAc的离解度为0.93%,求HOAc的离解常数。
解:(1)

(2)

从例1可以看出,对不同浓度HOAc溶液,在一定温度下,所计算出来的离解常数基本是一致的。表2-1是HOAc溶液在25℃时,不同浓度的离解度以及由离解度计算出来的离解常数值。
表2-1 25℃,不同浓度醋酸的离解度和离解常数
| 浓度/mol·L-1 | 离解度/% | 离解常数 |
| 0.001 | 12.4 | 1.76×10-5 |
| 0.01 | 4.1 | 1.76×10-5 |
| 0.02 | 2.96 | 1.80×10-5 |
| 0.1 | 1.32 | 1.76×10-5 |
| 0.2 | 0.93 | 1.76×10-5 |
利用离解常数可以计算一定浓度某弱酸溶液中的H+浓度,或计算弱碱溶液中的OH-=浓度。
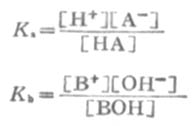
式中HA为弱酸,BOH为弱碱。
在浓度为c的弱酸中,[H+]=cα,即α=[H+]/c,又根据稀释定律,
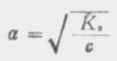
, 则
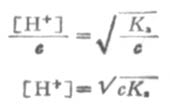
(2-3)
同理,在浓度为c的弱碱溶液中,
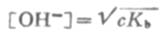
(2-4)
根据式(2-3)和式(2-4),可以计算一定浓度的弱酸或弱碱的[H+]或[OH-]。
离解常数的大小用以衡量酸或碱的强弱程度。酸或碱越弱,它们的离解常数值就越小。一般认为KI在10-5至10-9范围内的电解质是弱电解质;KI值小于10-10时是极弱电解质。
(二)影响离解平衡的因素
弱酸和弱碱的离解平衡都是暂时的、相对的动态平衡。当外界条件改变时,离解平衡像其它平衡一样,会发生移动,结果弱酸和弱碱的离解程度都有所增减。因此,可以应用平衡移动原理,通过改变外界条件,控制弱酸和弱碱的离解程度。外界条件主要指温度,同离子效应和盐效应的影响。
1.温度的影响
温度变化能使离解平衡发生移动,这种移动是通过离解常数的改变实现的,但在常温范围内变化不大。
2.同离子效应
离子浓度的改变,对弱酸和弱碱离解程度的影响极为显著。
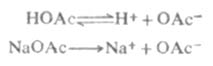
例如,在醋酸溶液中加入一些醋酸钠,由于醋酸钠是强电解质,在水溶液中完全离解Na+OAc-,这样溶液中[OAc-]增大,使

离解平衡向左移动,从而降低了醋酸的离解度和溶液中的H+浓度。
又如,在氨水中加入一些氯化铵,由于氯化铵是强电解质,在水溶液中完全离解成NH4+和CL-,这样溶液中[NH4+]增大,使离解平衡向左移动,从而降低了氨水的离解度和溶液中的OH-浓度。
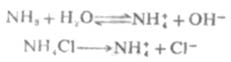
由此可以得出结论,在弱电解质溶液中,加入与弱电解质具有相同离子的强电解质,使弱电解质的离解度降低的效应,称为同离子效应。
3.盐效应
在弱电解质溶液中,加入与弱电解质没有相同离子的强电解质,而使弱电解质的离解度略微增大的效应,称为盐效应。
盐效应的产生,是由于强电解质的加入,使溶液中离子间的相互牵制作用增强,离子结合成分子的机会减少,降低了分子化的程度,因而达到平衡时,弱电解质的离解度比未加入强电解质时略微大些。
例如,在0.1mol·L-1HOAc溶液中加入NaCL晶体,使NaCL的浓度为0.1mol·L-1时,[H+]不是1.32×10-3mol·L-1,而是1.70×10-3mol·L-1,离解度不是1.32%而是1.70%.
应该指出,在发生同离子效应的同时,必然伴随着盐效应的发生.这两个效应对弱电解质离解度影响不同.盐效应可以使弱电解质的离解度增大一些,而同离子效应可以使弱电解质的离解度大大降低.这说明同离子效应和盐效应对溶液酸碱性的影响是不能相提并论的.因此,对稀溶液来说,如不考虑盐效应,是不会引起很大误差的.
二、多元酸碱在溶液中的离解
多元酸碱在溶液中的离解是分步进行的,叫做分步离解。表2-2列出了一些常见的多元酸的分步离解常数。表中pKa为Ka的负对数值。
表2-2 一些常见的多元酸的分步离解常数
| 名称 | 分子式 | Ka1 | PKa1 | Ka2 | PKa2 | Ka3 | PKa3 |
|
| 酸性强度增加 | 草酸 | H2C2O4 | 5.4×10-2 | 1.27 | 5.4×10-5 | 4.27 |
2.2×10-13 |
12.67 |
| 亚硫酸 | H2SO3 | 1.54×10-2 | 1.81 | 1.02×10-7 | 6.91 | |||
| 磷酸 | H3PO4 | 7.52×10-3 | 2.12 | 6.23×10-8 | 7.21 | |||
| 丙二酸 | CH2(COOH)2 | 1.38×10-3 | 2.86 | 2×10-6 | 5.70 | |||
| 邻苯二甲酸 | C6H4(COOH)2 | 1.12×10-3 | 2.95 | 3.9×10-5 | 5.41 | |||
| 酒石酸 | (CHOHCOOH)2 | 9.1×10-4 | 3.04 | 4.3×10-5 | 4.37 | |||
| 碳酸 | H2CO3 | 4.30×10-7 | 6.37 | 5.61×10-11 | 10.25 | |||
| 氢硫酸 | H2S | 9.1×10-8 | 7.04 | 1.1×10-12 | 11.96 |
例如草酸(H2C2O4)的离解分两步进行。
一级离解
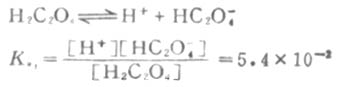
二级离解
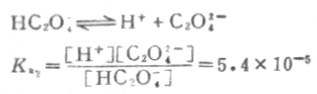
二级离解总比一级离解困难,因为H+要克服带有两个电荷的C2O2-4对它的吸引。从Ka1和Ka2可以反映这一点。草酸溶液中的HC2O-4浓度要比C2O2-4浓度大得多。
磷酸的离解要分三步,有Ka1、Ka2、和Ka3三个离解常数,且Ka1》Ka2》Ka3。这说明多元酸分级离解是依次变难。
根据多元酸的浓度和各级离解常数,可以算出溶液中各种离子的浓度。
例2 计算0.1mol·L-1H2S溶液中的H+和S2-的浓度。
解:由于H2S的 Ka1》Ka2 ,所以H2S溶液中的H+主要来自第一步离解,而第一步离解所产生的H+,又抑制第二步离解。这样计算H2S溶液中H+的总浓度时,可以忽略第二步离解的H+,近似地等于第一步离解平衡时H+浓度。
设第一步离解平衡时[H+]=x,则[H+]≈[HS-],平衡时则有下列关系:
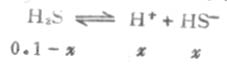
由表2-2知H2S的Ka为9.1×10-8,则
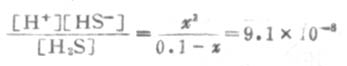
因Ka1很小,x必然很小,所以0.1-x≈0.1,则
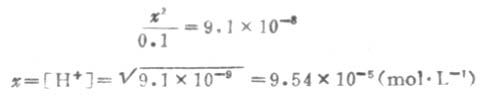
溶液中的S2-是第二步离解的产生,因此,计算溶液中的S2-浓度时,应根据第二步离解平衡进行计算.
设第二步离解时,[S2-]=y,平衡时有下列关系:
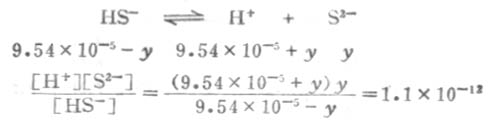
因为Ka1极小,y必然极小,所以9.54×10-5±y≈9.54×10-5,则
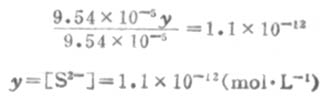
所以,[S2-]≈Ka2。
三、强电解质在溶液中的离解
(一)离子互吸学说
稀释定律适用于弱电解质溶液,而不适用于强电解质溶液。为了阐明强电解质在溶液中的实际情况,德拜(Debye)和休克尔(Huckel)提出了离子互吸学说,又叫完全电离学说。这种学说认为,强电解质在水溶液中完全离解成离子,离子在水溶液中并不完全自由。带异号电荷的离子相互吸引,距离近的吸引力大;带同号电荷的离子相互排斥,距离近的排斥力大。因此,离阳离子越近的地方,阳离子越少,阴离子越多;离阴离子越近的地方,阴离子越少,阳离子越多。总的结果是,任何一个离子都好像被一层球形对称的异号电荷离子所包围着。这层在中心阳离子周围所构成的球体,叫做离子氛。如图2-1所示,位于球体中心的离子称为中心离子,在中心阳离子周围有阴离子氛,在中心阴离子周围有阳离子氛。
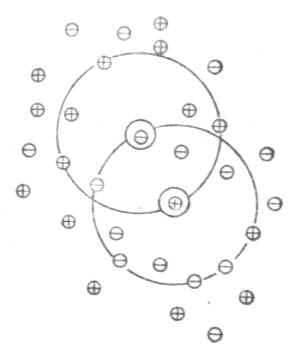
图2-1 离子氛示意图
在离子氛的影响下,溶液中的离子受到带有相反电离子荷氛的影响,而不能完全自由活动。使强电解质溶液中的离子不能百分之百地发挥应有的效能。因此,实测的离解度总是小于100%,这不是强电解质的真实离解度,它反映了溶液中离子间相互影响的程度,我们把这种离解度称为“表现离解度”。而强电解质的真实离解度是100%。
后来发现在强电解质溶液中,不但有离子氛存在,而且相反电荷的离子还可以缔合成离子对作为一个独立单位而运动。有的离子对没有导电能力。离子对在遇到强力碰撞时,可以分开,随后又可以重新形成新的离子时对。离子对的存在也使自由离子的浓度下降,导致溶液的导电能力下降。
离子氛和离子对的形成显然与溶液的浓度和离子电荷有关。溶液愈浓,离子所带的电荷愈多,上述效应愈显著。
如取不同浓度的KCL溶液,测定它的离解度(α)值,根据稀释定律求得相就的“离解常数”值如表2-3。
表2-3 18℃,不同浓度KCL溶液的“离解度”和“离解常数”
| 浓度/mol·L-1 | 离解度/% | 离解常数 |
| 0.01 | 94.2 | 0.152 |
| 0.1 | 86.2 | 0.536 |
| 1.0 | 75.6 | 2.34 |
| 2.0 | 71.2 | 3.52 |
由表2-3可以看出,强电解质”离解常数”K随溶液浓度的不同变化很大,这说明强电解质不存在离解常数.也就是说强电解质在溶液中是完全离解的,不存在离解平衡,因而就不存在离解度和离解常数.稀释定律是以弱电解质的可逆性过程为基础推导得出的,所以它不适用于强电解质溶液,不能客观地阐明强电解质在溶液中的实际情况.
(二)离子活动和活度系数
由于强电解质溶液中存在离子氛和离子对,每个离子不能完全自由地发挥它在导电等方面的作用,路易斯(Lewis)就提出了活度的概念.离子活度是溶液中离子的有效浓度.它等离子和活度系数的乘积.设离子的浓度为c,活度系数为f,则离子的活度(α)为:α=fc (2-5) 或f=α/c
活度系数f反映了离子间存在着相互影响这一因素.由于离子的活度一般都比浓度小,所以f一般都小于1.活度系数大,表示离子牵制作用弱,离子活动的自由程度大.溶液愈稀,活度系数愈接近于1.当溶液无限稀释时,活度系数等于1,这时离子的运动完全自由,离子活动就等于离子浓度.
因为电解质溶液中必定同时存在阳离子和阴离子,实验无法独测出阳离子的活度系数或阴离子的活度系数.但实验可以测出一个电解质的阳/阴离子的平均活度系数(f±).强电解质溶液的活度一般指溶液的平均活度(α±)
α±= f±×c
表2-4列举了25℃时,一些强电解质的离子平均活度系数.
表2-4 一些强电解质的离子平均活度系数(25℃)
| 电解质 | C/mol·L-1 | ||||||
| 0.001 | 0.005 | 0.01 | 0.05 | 0.1 | 0.5 | 1.0 | |
| HCL | 0.966 | 0.928 | 0.904 | 0.803 | 0.796 | 0.758 | 0.809 |
| KOH | 0.96 | 0.92 | 0.90 | 0.82 | 0.80 | 0.73 | 0.76 |
| KCL | 0.965 | 0.927 | 0.901 | 0.815 | 0.769 | 0.651 | 0.606 |
| H2SO4 | 0.630 | 0.639 | 0.544 | 0.340 | 0.265 | 0.154 | 0.130 |
| Ca(NO3)2 | 0.88 | 0.77 | 0.71 | 0.54 | 0.48 | 0.38 | 0.35 |
| CuSO4 | 0.74 | 0.53 | 0.41 | 0.21 | 0.16 | 0.068 | 0.047 |
例3 已知25℃时,0.1mol·L-1KCL溶液中,离子的平均活度系数为0.769,求离子的平均活度.
解:已知f±=0.769 c=0.1 mol·L-1
α±=0.769×0.1=0.0769×mol·L-1
(三)离子强度
溶液中离子的活度系数不仅与它的浓度有关,并且还与溶液中其它各种离子的总浓度和离子的电荷数有关,但与离子的种类无关.因此,溶液中离子的浓度和离子的电荷数就成为影响离子活度系数的主要因素.为了阐明离子浓度和离子电荷数对离子活度的影响,引入了离子度的概念.离子强度表示溶液中离子所产生的电场强度.它是溶液中各种离子的量浓度乘以离子电荷数的平方总和的二分之一
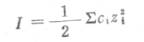
(2-6)
式中,I代表溶液的离子浓度;c是离子的量浓度;z是离子的电荷数.
例4 求0.01mol·L-1NaCL溶液的离子强度.
解:I=1/2×(0.01×12+0.01×12)=0.01
例5 溶液中含有0.05mol·L-1NaCL和0.01 mol·L-1KCL,求该溶液的离子强度.
解:I=1/2×(0.05×12+0.05×12+0.01×12+0.01×12)=0.06
离子活度系数随溶液中离子强度的改变而显著改变,表2-5列出了离子强度和平均活度系数的关系.溶液中离子强度越大,离子间的相互影响越强,离子活动受到的限制就越大。只有当溶液接近于无限稀释时,离子强度趋近于零,离子才能完全自由活动,这时离子的活度生活费数就接近于1,即离子活度就接近于离子的真实浓度。
表2-5 不同离子强度时离子的活度系数(25℃)
| 活度系数
离子强度 | 电 荷 数 | |||
| 1 | 2 | 3 | 4 | |
| 1×10-4 | 0.99 | 0.95 | 0.90 | 0.83 |
| 2×10-4 | 0.98 | 0.94 | 0.87 | 0.770.77 |
| 5×10-4 | 0.97 | 0.90 | 0.80 | 0.67 |
| 1×10-3 | 0.96 | 0.86 | 0.73 | 0.56 |
| 2×10-3 | 0.95 | 0.81 | 0.64 | 0.45 |
| 5×10-3 | 0.92 | 0.72 | 0.51 | 0.30 |
| 1×10-2 | 0.89 | 0.63 | 0.39 | 0.19 |
| 2×10-2 | 0.87 | 0.57 | 0.28 | 0.12 |
| 5×10-2 | 0.81 | 0.44 | 0.15 | 0.04 |
| 0.1 | 0.78 | 0.33 | 0.08 | 0.01 |
| 0.2 | 0.70 | 0.24 | 0.04 | 0.003 |
| 0.3 | 0.66 | 0.62 | - | - |
| 0.5 | 0.62 | - | - | - |
采用离子强度的目的,是因为离子的活度系数的测定方法一般比较复杂,不容易测定。但是,离子活度系数与离子强度间却存在着一定的联系,并且离子强度很容易由离子的浓度与其所带电荷而求得。在测定离解迷路数时等精密工作中,要求对离子的有效浓度作精确计算,这就需要由离子将浓度换算成活度。但在一般有关稀溶液的计算中,可直接换算成活度。
